|
碰撞检测是三维游戏中不可或缺的一部分。试想一下如果没有碰撞检测,在CS游戏里我们将穿墙而过,子弹不会击毙敌人,无法上楼梯等。所以要实现较为真实的游戏场景,碰撞检测是不可缺少的。下面简单分析一下相机与世界进行碰撞检测的过程。在移动相机(就是移动观察点)以前,首先必须判断相机将要进入的区域是否允许进入,如果允许,就将相机的位置移动到将要进入的区域;反之,将查找什么位置发生了碰撞,并对发生的碰撞做出响应。
由于将遍历世界模型中的所有三角形的,所以下面只讨论单个三角形。
一 、三角形所在平面与摄像机球体的位置关系
三角形与摄像机的位置关系分为相交和不相交,而不相交又分为在三角形的正面或者背面,在三角形的正面或者背面是根据三角形的法线向量来决定的,所以第一步先求出三角形的法线向量。
CVector3 vTriangle[3] = { pVertices[i], pVertices[i+1], pVertices[i+2] };
这里定义了一个三个元素的数组,每个元素代表三角形的一个顶点。
CVector3 的定义很简单,详细情况请参看源代码。
下面的代码计算三角形的法线向量
CVector3 vNormal = Normal(vTriangle);
CVector3 Normal(CVector3 vPolygon[])
{
// 获取三角形两个边的的向量
CVector3 vVector1 = vPolygon[2] - vPolygon[0];
CVector3 vVector2 = vPolygon[1] - vPolygon[0];
// 对两个边的向量进行叉乘操作,结果即为三角形的法线向量
CVector3 vNormal = Cross(vVector1, vVector2);
// 归一化向量
vNormal = Normalize(vNormal);
return vNormal;
}
定义一个变量来保存球体中心到三角形所在平面的距离。
float distance = 0.0f;
然后,判断三角形与球体的关系,相交、在正面或者在背面。同时也得到了球体到三角形所在平面的距离。
int classification = ClassifySphere(m_vPosition, vNormal, vTriangle[0], m_radius, distance);
以下是ClassifySphere函数的定义:
int ClassifySphere(CVector3 &vCenter,
CVector3 &vNormal, CVector3 &vPoint, float radius, float &distance)
{
// 首先我们获取平面到坐标原点的距离,这里我们用到了平面的一般方程
// Ax + By + Cz + D = 0,则D = -(Ax + By + Cz),D即为平面到原点的距离。
float d = (float)PlaneDistance(vNormal, vPoint);
// 下面为点到平面的距离公式
distance = (vNormal.x * vCenter.x + vNormal.y * vCenter.y + vNormal.z * vCenter.z + d);
// 如果上面得到的距离的绝对值小于球体的半径则认为球体与三角形所在平面相交。
if(Absolute(distance) < radius)
return INTERSECTS;
// 如果distance >= radius,则球体在三角形的正面,注意distance有符号。
else if(distance >= radius)
return FRONT;
// 如果都不是,则球体在三角形的背面。
return BEHIND;
}
通过以上步骤就可以判断出球体和三角形的位置关系,这为进一步计算球体与三角的接触点奠定了基础。
二、计算摄像机球体与三角形所在平面的接触点
如果上面一步ClassifySphere函数的返回值是相交的话,需要计算摄像机球体与三角形所在平面的接触点。
// 这里可能需要一些线性代数的基础。
// 下面一行得到的向量是从接触点指向球心的
CVector3 vOffset = vNormal * distance;
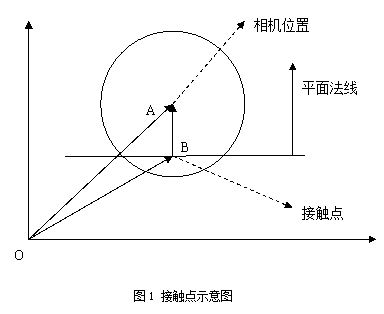
// 从位置向量中减去上面的向量就得到了接触点,如图1所示。A为相机位置,B为接触点位// 置。向量OA减去向量BA得到向量OB,B点就是要求的接触点。
CVector3 vIntersection = m_vPosition - vOffset;
三、判断接触点是否在三角形内
上面已经得到了球体与三角形所在平面的接触点,接下来判断接触点在不在三角形的区域内,区域包括三角形内部和边缘。首先,判断接触点是否在三角形的内部。这个问题比较简单,把接触点和三角形的三个顶点分别连接,然后计算这些连线的夹角之和,如果等于360度就认为点在三角形内部,否则认为点在三角形区外部,如图2所示。
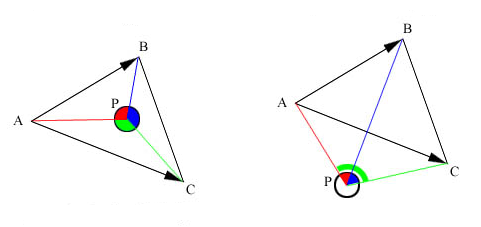
图2 点是否在三角形内的示意图
这个方法简单易行但是由于用到了比较费时的反三角函数所以效率稍低,读者可以改用射线法,或者向量法来提高效率。下面的函数用来判断点是否在三角形的内部。
bool InsidePolygon(CVector3 vIntersection, CVector3 Poly[], long verticeCount)
{
// 我们在判断夹角之和是否为360度时,由于计算机的精度限制,不可能正好360度,// 所以我们用MATCH_FACTOR来表示与360的接近程度。
const double MATCH_FACTOR = 0.99;
double Angle = 0.0;
CVector3 vA, vB;
for (int i = 0; i < verticeCount; i++)
{
vA = Poly[i] - vIntersection;
vB = Poly[(i + 1) % verticeCount] - vIntersection; Angle += AngleBetweenVectors(vA, vB);
}
if(Angle >= (MATCH_FACTOR * (2.0 * PI)) )
return true;
return false;
}
下面的代码用来判断点是否在三角形的边上。
bool EdgeSphereCollision(CVector3 &vCenter,
CVector3 vPolygon[], int vertexCount, float radius)
{
CVector3 vPoint;
// 遍历所有的多边形顶点
for(int i = 0; i < vertexCount; i++)
{
// 找出一条边上离球心最近的点,在下面将详细解释
vPoint = ClosestPointOnLine(vPolygon[i], vPolygon[(i + 1) % vertexCount], vCenter);
// 计算球心到该点的距离
float distance = Distance(vPoint, vCenter);
// 如果距离小于半径则球体与三角形的边有接触
if(distance < radius)
return true;
}
return false;
}
找出一条边上离球心最近的点需要考虑两种种情况,如图3所示。
图3 点和线段的两
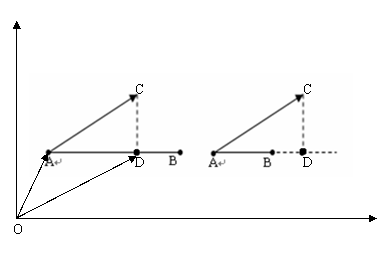
种位置关系
图3中A,B为线段的两个端点,C为球心点,D点为C点的投影点,图3左边的这种情况下,将向量AC投影至向量AB得出向量AD,向量OD等于向量OA加向量AD,D点即为所求点;图3右边的这种情况下,B点即为所求点。核心代码如下:
CVector3 ClosestPointOnLine(CVector3 vA, CVector3 vB, CVector3 vPoint)
{
CVector3 vVector1 = vPoint - vA;
// 得出向量AB的单位向量
CVector3 vVector2 = Normalize(vB - vA);
// 计算线段长度
float d = Distance(vA, vB);
// 利用点乘进行投影
float t = Dot(vVector2, vVector1);
if (t <= 0)
return vA;
if (t >= d)
return vB;
// 构造向量AD
CVector3 vVector3 = vVector2 * t;
// 计算OD
CVector3 vClosestPoint = vA + vVector3;
return vClosestPoint;
}
至此,碰撞检测的工作完成了。
四、对碰撞的响应
对碰撞的响应我们没有简单地采取停止摄像机运动的方式,而是采用了沿碰撞平面滑动的方式,原理如图4所示。

图4 沿墙滑动原理图
CVector3 GetCollisionOffset(CVector3 &vNormal, float radius, float distance)
{
CVector3 vOffset = CVector3(0, 0, 0);
// 一旦我们发现了碰撞的发生,我们必须确保我们的摄像机不至于进入到墙体。在我// 们的程序里摄像机的确进入了墙体,但是我们在渲染场景以前就进行了碰撞检测,// 这样就消除了摄像机跳跃的现象。
// 通常的情况下,您仅仅需要考虑正面的碰撞,但是如果你不需要背面剔除你就必须// 对正反两面的碰撞进行处理。
if(distance > 0)
{
float distanceOver = radius - distance;
vOffset = vNormal * distanceOver;
}
else
{
float distanceOver = radius + distance;
vOffset = vNormal * -distanceOver;
}
return vOffset;
}
// 更新视点位置
m_vPosition = m_vPosition + vOffset;
m_vView = m_vView + vOffset;
程序的运行效果如图5所示。
图5 程序运行截屏
五、结语
以上的代码在VC6.0开发环境下编译通过,程序运行流畅,比较逼真地模拟了三维空间的漫游并加入了碰撞检测及响应。以上的算法中用到了比较多的线性代数知识,读者可以参阅相关书籍以加深理解。
|