|
一、前言
在基于Windows平面图像的处理技术中,图像的旋转功能是频繁使用的基本功能之一,很多计算机图形图像处理软件都具备了该项功能,如PhotoShop、CoreDraw、MS Office等,软件用户可方便快捷地处理图像文件。但有些软件,如Windows自带的“画图”程序(MSPaint),在旋转图像时功能就很欠缺,不仅不能实现图像的任意角度旋转,而且旋转过程和结果不直观便捷,且无法控制。目前,随着国内计算机的快速普及,软件用户对图像处理的需求也越来越多,对软件的图像处理能力、方便性和易用性都提出了一定的要求。如何满足这些需求,是程序设计人员必须关注和考虑的。
所谓“交互式、可控制图像旋转”,就是利用计算机交互式设备,如鼠标、手写笔、触摸屏等设备,用户可以以手动方式,非常直观地对需要处理的图像进行任意角度的旋转,而且在旋转过程中,用户也可以直接看到当时的旋转效果,便于用户操控。本文就计算机平面图像的交互式、可控制旋转问题加以讨论,并提出相应的实现方法和程序实例。
二、原理
计算机图像旋转问题无论在理论还是实现方法上,都已经非常成熟,本文不再加以深入阐述,只是就涉及到的原理和方法进行简单的说明。主要将针对交互式的旋转问题进行讨论,并给出实现方法。
1. 图像旋转几何原理
由于计算机输出设备的特点,平面图像的显示,都是转换成相应的矩形点阵加以显示或打印,因此,计算机的图像处理,主要是对矩形点阵中的“点”进行处理。一般我们将计算机图像的旋转归类到计算机图像几何范畴中。
如图1所示:矩阵中的某点A[x1,y1],绕圆心旋转θ角度后,位置为B[x2,y2]。根据三角函数向量计算可得这两点的位置关系为:
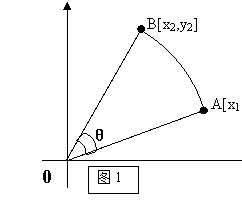
x2 = x1cosθ - y1sinθ
y2 = x1sinθ + y1cosθ
根据矩阵原理,将一点的变换归纳应用于整个矩形点阵,从而推导出其矩阵公式。在实际计算中,一般采取从目标点计算出原点坐标,再按原点坐标将其颜色值赋值到目标点。这样,可以避免计算中取整造成的颜色丢失。其矩阵公式为:

具体可参考实例中BitMap_Rotate()代码段所示。
2.交互式平面图像旋转实现原理
如前所述,在一般的图像处理中,通过使用鼠标、指点设备和触摸屏方式,方便用户操作计算机软件。那么,平面图像的旋转如何实现这些功能呢?
(1)实现方式设计
在Windows开发中,以设备为例,对鼠标设备的各种操作,都可以通过事件方式捕获,并对该事件进行编码,以实现相应的功能,如鼠标的移动、鼠标键的按下抬起,鼠标的拖动(指功能键保持按下,同时移动鼠标)。图像旋转时,用户可以在图片上按下鼠标左键不放,并沿着旋转方向拖动鼠标,使图片产生旋转;当用户释放鼠标左键后,旋转过程立即结束。
因此,我们可以这样设计程序:
1)当鼠标按下,对鼠标的坐标位置进行取样,记入原点坐标。
2)当鼠标拖动时,捕获鼠标新的位置坐标,并与原点坐标进行计算,得到旋转角度。
3)根据旋转角度,对图像进行旋转。
4)当鼠标按键抬起时,结束旋转操作。
在Windows的鼠标事件中,可以使用的鼠标事件主要有:
1)OnMouseDown 事件――捕获原点坐标。
2)OnMouseMove 事件――捕获目标点坐标,并计算旋转角度,然后按角度旋转图片。
3)OnMouseUp 事件 ―― 结束旋转操作,停止相关处理。
(2) 旋转几何角度的计算
当鼠标拖动时,可以捕获到原点坐标和目标点坐标,通过对位置的几何计算,从而获得旋转的角度。
如图2所示,点A[x1, y1]代表鼠标按键按下时的指针位置,其角度为α1;当鼠标拖动到点B[x2, y2]后,其角度为α2。所以,点A到点B之间的矢量夹角θ就是旋转角度。
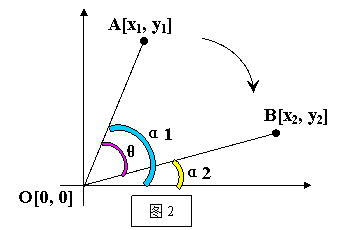
θ = α1-α2
根据三角函数原理,可以得到:
Tan(α1) = (y1 / x1 )
Tan(α2) = (y2 / x2 )
Tan(θ) = Tan(α1 - α2)
= (Tanα1 - Tanα2) / (1 + Tanα1 * Tanα2)
= (y1 x2 - y2 x1) / (x1 x2 + y1 y2)
再根据反三角函数公式,可以得到:
θ = ArcTan( (y1 x2 - y2 x1) / (x1 x2 + y1 y2) )
也可以直接利用反三角函数,分别求出α1和α2,相减得出θ。
α1 = Arctan(y1 / x1 )
α2 = Arctan(y2 / x2 )
θ = α1-α2 = Arctan(y1 / x1 ) - Arctan(y2 / x2 )
考虑到旋转方向和坐标象限,在旋转前将θ的值取负值,即:
θ = -θ
最后,将角度值θ赋值给旋转函数,作为旋转的角度,操作旋转实现即可。
(3)程序实现
程序以Delphi7编写(详见实例RotByMouse),使用Delphi7自带的标准控件完成,不需要安装其它第三方控件。在Image1控件的几个鼠标事件中添加旋转操作的控制代码,如下:
1)MouseDown 事件
鼠标按键落下时,捕获鼠标位置,作为起始点,并利用反三角函数公式并转化成起始角度。注意,Delphi中ArcTan2()函数返回值为弧度值,弧度值与角度值的转换关系为:角度= (180/π) * 弧度。另外,事件处理中要考虑到特别位置,如图像的矩形中心位置的处理。
procedure TForm1.Image1MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
//条件: 按住鼠标左键, 并非双击鼠标时
if (Button = mbLeft) and not (ssDouble in Shift) then
begin
RotState := True;
StartTheta := 0;
Ag := 0 ;
if X = Image1.Width / 2 then
if Y < Image1.Height / 2 then
StartTheta := Pi / 2
else
StartTheta := -Pi / 2
else
StartTheta := ArcTan2(Y - Image1.Height / 2, X - Image1.Width / 2);
end
else
begin
RotState := False;
end;
end;
2)MouseMove事件
当鼠标拖动时,捕获鼠标新的位置,计算出新的旋转角度,并减去起始角度,得到图像的旋转角度值,并操作图像旋转。
procedure TForm1.Image1MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
var
Theta, Angle: Extended;
begin
//条件: 按住鼠标左键, 并非双击鼠标时,参考 Image1MouseDown事件
if RotState then
begin
if X = Image1.Width / 2 then
if Y < Image1.Height / 2 then
Theta := Pi / 2
else
Theta := -Pi / 2
else
Theta := ArcTan2(Y - Image1.Height / 2, X - Image1.Width / 2);
Angle := 180 * (StartTheta - Theta) / Pi;
Ag := Angle;
Rotate; //旋转图像
Update;
end;
end;
3) MouseUp 事件
当鼠标按键抬起后,则停止图像旋转的操作。
procedure TForm1.Image1MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
if RotState then
begin
RotState := False;
StartTheta := 0;
Ag := 0 ;
end;
end;
另外,图像旋转函数可参见BitMap_Rotate( )函数,图3 是程序运行效果。
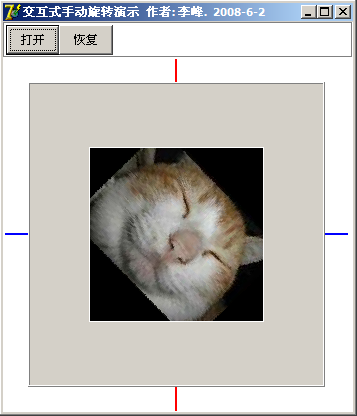
图3 运行效果图
通过以上分析和设计,可以实现图像交互式、任意角度的旋转。旋转效果非常流畅和稳定,方便用户在使用中的操作。
|