摘  要  在计算器的设计中，加、减、乘、除和括号功能是有优先级的，括号优先于乘除，乘除优先于加减，实现了这部分功能，就完成了计算器的主要框架的设计，在此基础上就可扩充其它的功能，如各种函数功能。

关键词 计算器，加、减、乘、除、括号，优先级

所使用的计算器一般具备加、减、乘、除功能，好一点的计算器还具有括号功能，使计算器能完成较复杂一些的设计，更好一点的计算器还具有各种函数功能，使计算器用起来更加实用和方便。总之，加、减、乘、除功能和括号功能是科学计算器所必须具有的功能，在此基础上可以很容易地扩充各种函数功能，如sin、cos、tan、log、lnx、xⁿ等等，以实现复杂的运算。

一、       优先功能

任何一个计算表达式，如a＋b×c÷( d－e×f＋g )－h，计算的规则是：先乘、除后,加、减，遇到括号先执行括号里的表达式，并且括号里的表达式同样遵循这一原则。因此，要获得正确的运算结果，首先是如何来实现先乘除后加减呢？这就要对操作符定义一个优先级，即谁先执行，而操作符的优先级通常是用自然数来表示的，称为优先数。＋、－的优先数小于×、÷的优先数，而×、÷优先数小于括号〔  〕，等号“＝”的优先数最低，低于＋、－的优先数；由于在一个计算表达式中既有操作数（整数或实数等）和操作符（＋、－、×、÷、＝等），还有操作符的优先数，这就至少需要二个堆栈，一个是暂存操作数或中间结果的堆栈，简称操作数栈；另一个是暂存操作符优先数的堆栈，称为操作符栈。为了编程的方便，这里操作符栈用了二个，一个用于暂存操作符的字符堆栈，另一个用于暂存操作符优先数（自然数）的堆栈。三个堆栈的栈深M取为常数，这里取M=50，用定长数组来表示，可保证堆栈不会出现上溢，当然用可变数组或链栈来表示则最好。

加、减的优先数，用整数int ADD=SUB=1来表示；乘、除的优先数用整数int MUL=DIV=2来表示。当然你可以取其它整数来表示，只要乘、除的优先数大于加、减的优先数即可。等号的优先数最低，用int EQU=0来表示。从上述表达式可看出，左括号“（”的优先数高于左边操作符的优先数，而低于右边操作符的优先数，这样一个左括号就有二个优先数，这样会使编程复杂化，因此须对左括号作特殊处理：就是遇到左括号直接压栈，而不做优先数的比较。另外，为了保证左括号右边的操作符能正常压栈，因此，左括号的优先数应低于加、减操作符的优先数，即左括号的优先数应取为int LPARENT=0；而对右括号的处理是：右括号一律不进栈。

实现加、减、乘、除和括号功能的算法步骤：首先从左向右读取计算表达式，读一个操作数或一个操作符，统称为读一个单词。

⑴ 从左向右扫描表达式，读一个单词。

1）当前单词是操作数，压栈；继续本步。

2）当前单词是操作符，则转⑵。

3）当前单词是左括号“（”，则转⑶。

4）当前单词是右括号“）”，则转⑷。

5）当表达式扫描完毕，即单词是等号，则转⑸。

⑵ 若操作符栈空，则操作符进栈，转⑴；若操作符栈不空，则比较当前操作符与栈顶操作符的优先数。

1）  当前操作符优先数大，则当前操作符进栈，转⑴。

2）  当前操作符优先数小于或等于，则操作符栈栈顶操作符退栈，同时操作数栈出栈二个操作数，运算后结果进操作数栈；如当前操作符是＝或（＋或－），则继续本步操作；否则，转⑴。

（3）左括号“（”进操作符栈，转⑴。

⑷ 检查操作符栈：

1）若栈顶是左括号“（”，则左括号退栈，转⑴。

2）若栈顶不是左括号“（”，则栈顶操作符出栈，同时操作数栈出栈二个操作数，运算后结果进操作数栈，继续重复本步操作。

3）  栈中没有配对的左括号，则按出错处理。

⑸ 检查操作符栈。

1）若栈不空，则栈顶操作符出栈，同时操作数栈出栈二个操作数，运算结果进操作数栈，继续重复本步操作。

2）  栈空，这时操作数栈顶元素即为最终计算结果。

算法流程图见图1

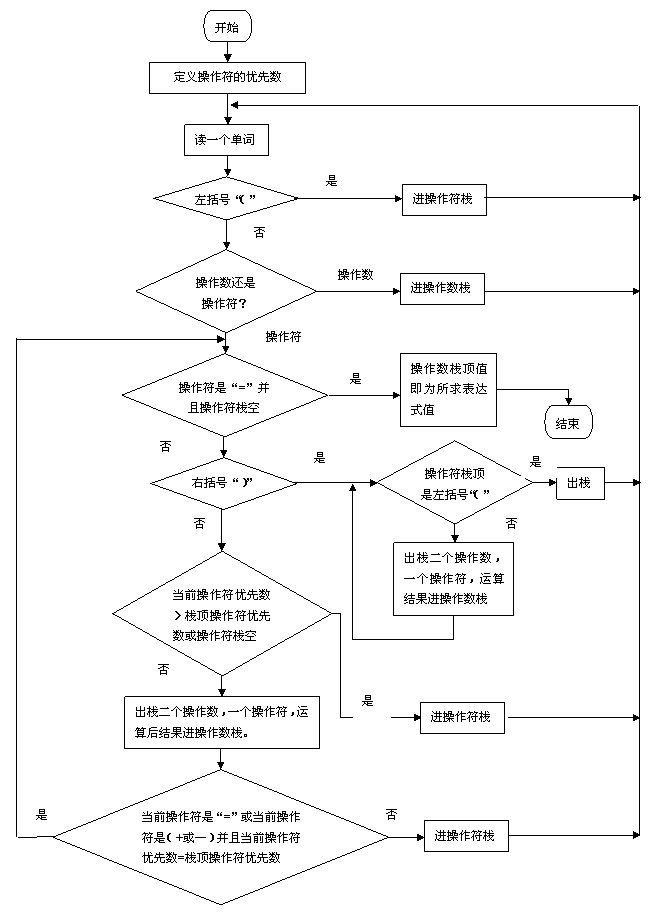
图1算法流程图